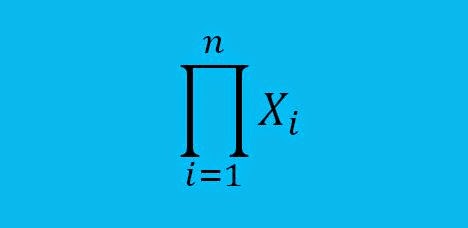How to Write a Simple Algorithm Using Pseudocode | Example Nine

Outline the pseudocodes that will request for an integer number n, and n different numbers Xi, afterwards it will calculate and display the product of all the Xi numbers,

Product Operator

Premise:

The formula above is a product operator just like the summation operator "Sigma". i=1 means that we are start from one; the n means that we will stop at the value of n. Xi is the numbers which we are told to find their product. That is i run from one (1) to n (whatever the value be, will be the end point). What is even running from one to n? Of course you are right Xi!

Solution:

Major Steps
1. Request Data
2. Calculate product
3. Display Product
Stepwise Refinement
1. Request Data
    1.1 Request n
2. Determine score
    2.1 Product = 1
    2.2 count = 0
    2.3 Request Xi
    2.4 Product = product * Xi
    2.6 Repeat 2.3 and 2.4 until count < n
3. Display product

Explanation:

In this example i believe that you are familiar with most steps here except step 2.1, 2.2 and 2.6.
You have to initialise the product variable to the value one, because if the first value Xi is:

Xi = 3.

At line 2.3, then at line 2.4 we will have that the product will be the initial value of product multiply by the value Xi:

Product = 1 * 3 = 3.

Note that if I had initialise the product to be zero (0), you should know as a mathematician that anything multiply by zero (0) is Zero and the algorithm will be meaningless since will still end at zero for the n values.
If the second value is Xi = 4, then the product will be the previous product multiply by the value of Xi:

Product = 3 * 4 = 12.

The process will continue until the algorithm reaches the value of n which step 2.6 takes care off.
Line 2.2 say; count = 0, if you remember we have used count = 1; in example five. These two initialisations are difference, the way we use them both in algorithm development and programming differs.
When you use count = 1, it means that you are starting your count from the value one (1), and line 2.6 makes sure that you are still counting until count <= n.
Instance One: If n = 4, the algorithm will run from i to n (1 to 4), because it will be counting like this:

1, 2, 3, 4.

Thus 4 items/numbers will count. That is four (4) times the algorithm requested and accepted Xi.
When you use count to be: count = 0, it means that you are staring your count from the value zero (0), and line 2.6 makes sure that you are still counting until count < n.
Instance Two: If n = 4, the algorithm will run from "i to n - 1" (0 to 3), why? Because it will count in this form:

0, 1, 2, 3.

Thus 4 items/numbers as above. So here count will stop when count is 1 < n. Here 3 is 1 < 4 (i.e 3 = 4 - 1), how? Because 3 + 1 = 4. So removing the 1 makes 3 to size to be four again and that is why in line 2.6 i used count < n ( i.e. count = n - 1).
Note that in some cases count may not be initialise to 0 but 1 or any other number, it depend on the demand of the algorithm, such that the product can be change to count and count can be change to product while maintaining what each variable does or hold (i.e. each of the variables should hold the right constants.
Always name your variables to represent what they do, it is important in programming. Instead of using 'i' like other programmers, I make use of "count" so that no matter how large the algorithm is I will always remember that I use count to count.
So you have to always remember these rules, that when:

1. Starting point is: count = 1 ending point is: count <= n,
2. Starting point is: count = 0 ending point is: count < n.

Where n can be any variable that can hold an integer value.
Contrary to the above rules there will be error in the algorithm.
In 1 above, removing the equality '=' sign (1. starting point is: count = 1 ending point is: count < n) will cause the algorithm time of execution to be equal to the time it will take an astronomer to travel from this universe to another universe. In other words the person/device obeying/performing the step(s) will be doing it until infinity.
In 2 above, if you add equality sign at the back of the less than (2. starting point is: count = 0 ending point is: count <= n), then count will end at n + 1. That is, if n is supposed to be: 0, 1, 2, 3 then it will be; 0, 1, 2, 3, 4. that is 5 items/numbers/counts which is error.
Copy the rules into your record book because we will be making use of them in all our algorithms and programmes.

Previous: Example Eight    |    Next: Example Ten

SHARE THIS POST WITH YOUR FRIENDS...::

Tweet